Justifications that eⁱ = cos() + i sin()

Justification #1: from the derivative

Consider the function on the right hand side (RHS)
    f(x) = COs( x ) + i sin( x )

Differentiate this function
    f ' (x) = -sin( x ) + i COs( x) = i f(x)

So, this function has the property that its derivative is i times the original function.
What other type of function has this property?

A function g(x) will have this property if
    dg / dx = i g
This is a differential equation that can be solved with separation of variables
    (1/g) dg = i dx
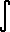    (1/g) dg = 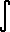i dx
    ln| g | = i x + C
    | g | = e^{i x + C} = e^C e^{i x}
    | g | = C₂ e^{i x}
    g = C₃ e^{i x}

So we need to determine what value (if any) of the constant C₃ makes g(x) = f(x).
If we set x=0 and evaluate f(x) and g(x), we get
    f(x) = COs( 0 ) + i sin( 0 ) = 1
    g(x) = C₃ e^{i 0} = C₃
These functions are equal when C₃ = 1.

Therefore,
    COs( x ) + i sin( x ) = e^{i x}

Justification #2: the series method

(This is the usual justification given in textbooks.)

By use of Taylor's Theorem, we can show the following to be true for all real numbers:

sin x = x - x³/3! + x⁵/5! - x⁷/7! + x⁹/9! - x¹¹/11! + ...

COs x = 1 - x²/2! + x⁴/4! - x⁶/6! + x⁸/8! - x¹⁰/10! + ...

e^x = 1 + x + x²/2! + x³/3! + x⁴/4! + x⁵/5! + x⁶/6! + x⁷/7! + x⁸/8! + x⁹/9! + x¹⁰/10! + x¹¹/11! + ...

Knowing that, we have a mechanism to determine the value of eⁱ, because we can express it in terms of the above series:

e^(i) = 1 + (i) + (i)²/2! + (i)³/3! + (i)⁴/4! + (i)⁵/5! + (i)⁶/6! + (i)⁷/7! + (i)⁸/8! + (i)⁹/9! + (i)¹⁰/10! + (i)¹¹/11! + ...

We know how to evaluate an imaginary number raised to an integer power, which is done as such:

i¹ = i
i² = -1     terms repeat every four
i³ = -i
i⁴ = 1
i⁵ = i
i⁶ = -1
etc...

We can see that it repeats every four terms. Knowing this, we can simplify the above expansion:

e^(i) = 1 + i - ²/2! - i³/3! + ⁴/4! + i⁵/5! - ⁶/6! - i⁷/7! + ⁸/8! + i⁹/9! - ¹⁰/10! - i¹¹/11! + ...

It just so happens that this power series can be broken up into two very convenient series:

e^(i) =
  [1 - ²/2! + ⁴/4! - ⁶/6! + ⁸/8! - ¹⁰/10! + ...]
+
  [i - i³/3! + i⁵/5! - i⁷/7! + i⁹/9! - i¹¹/11! + ...]

Now, look at the series expansions for sine and cosine. The above above equation happens to include those two series. The above equation can therefore be simplified to

e^(i) = COs() + i sin()

An interesting case is when we set = 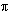, since the above equation becomes

    e^(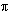 i) = -1 + 0i = -1.

which can be rewritten as

    e^(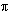 i) + 1 = 0.     special case

which remarkably links five very fundamental constants of mathematics into one small equation.

Again, this is not necessarily a proof since we have not shown that the sin(x), COs(x), and e^x series converge as indicated for imaginary numbers.

 
Contact us | Advertising & Sponsorship | Partnership | Link to us

© 2000-2023 Math.com. All rights reserved.     Legal Notices.     Please read our Privacy Policy.